How to Eat Eggs

How should you eat your eggs?

I don’t mean sunny-side up or scrambled or as an omelette. I’m asking which order you should remove them from the carton. See, a while back the internet exploded over whether left-to-right or right-to-left was the “correct choice”¹.

Eventually some people started to insist that from the centre out was the only option to “preserve balance”. But is it?

A colleague and I were discussing this today² and realised there is a nice little puzzle here. In the UK, where I live, the most common egg carton is a 2 ✕ 3 pack of six eggs. If I want to remove the eggs from the carton one at a time such that the centre of gravity never strays too far from the centre of the box, which order should I remove them in?

Its worth taking a moment and finding the answer by hand as we did before reading on. Its a fun little puzzle with a not-too-difficult solution that can easily be found with pen and paper. We solved it on the blackboard and then I went away and coded a solution in Mathematica to try reteach myself the language.

If you’re ready for the solution, here we go.

Graphics elements

We start with some boilerplate in Mathematica in order to draw eggs in cartons. This will make working with the problem a bit more pretty and easy to see. You can skip this section if you don’t really care about visuals.

Lets start out with a neat little egg carton to place our eggs in.

It will be useful to put our eggs in the cartons like so:

We also need a helper function to draw these pictures in graphs. Don’t worry about this too much: all it does is draw the above image in the right place at the right size.

Eggs

If there are 6 places in the carton, each of which can hold an egg or not, there are \(2^6 = 64\) possible configurations of eggs in our carton:

The weight of a configuration is simply the number of eggs in the carton.

In particular, we have full and empty configurations where the carton holds six or no eggs.

We could go ahead and work with these configurations, but the situation we are in is highly symmetric. If we are interested in how unbalanced the egg carton is, we don’t really care if its unbalanced to the left or to the right. All we care about is how big the imbalance is.

Mathematically, we say that we have the symmetries of \( C_2 \times C_2 \). That is to say that you can reflect the box over the \( x \) or the \( y \) axes and not really end up with a new configuration. You may think we can also rotate the box, but if you rotate it a quarter turn then the long and short edges don’t match and if you rotate it a half turn, this is actually the same as doing a reflection about the \( x\) and \(y\) axes!

Lets make a function that gives us all these configurations. We sort them (arbitrarily) to make comparison easy.

If we now only count configurations up to their symmetries, we have far fewer to deal with.

For example, the following egg configurations are actually related by a symmetry :

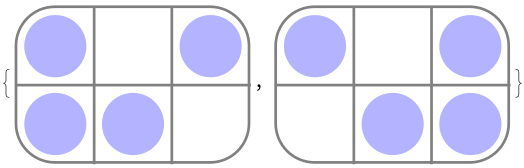
You can check that this is the complete list of representative configurations. Every carton is either one of these boxes or a reflection about the \( x \) or \( y \) axis.

To see if you can remove an egg from a configuration to make another one, we have to do some work. Firstly, we define the distance between two configurations (without symmetries) as the number of eggs you’d have to add or remove to go from one to the other (this is known as the Hamming Distance). Note that we aren’t allowed to move eggs around the carton!

Then we allow ourselves to rotate and reflect the carton to work out the distance between two configurations or any of their symmetries.

Finally we can say that you can remove an egg from a configuration to get a second configuration if they have distance one and the first configuration has more eggs (higher weight) than the second.

If you think that seems like an incredibly complicated way to describe that, you’d be right, but unfortunately its the easiest way to describe the situation to a computer and a reasonable mathematical definition. In the end, though, we are rewarded with an airtight definition/algorithm for determining if you can get from one configuration (or its symmetries) to another by removing an egg.

Graphs

As mentioned, there are a lot of configurations. If we draw a graph where each node (vertex) is one egg carton configuration and there is an edge from carton \(A\) to carton \(B\) if you can remove a single egg from \(A\) to get \(B\) we get this:

Ouch!

However, remember we don’t care about the symmetries so we replace this graph with the one where the nodes are the representatives of the symmetric configurations. We’ll call this graph the “egg graph”, or \( EG \) for short.

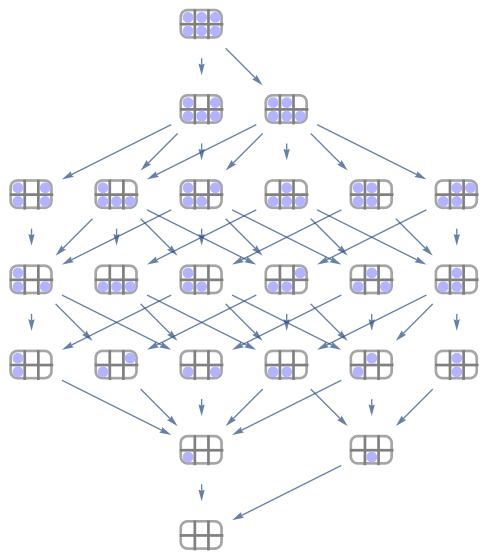
That’ s much neater!

What have we done now? We have listed all the possible ways to remove eggs from a carton, one by one, until they are empty up to symmetries. They are exactly all the paths in that graph from the top node (the full box) to the bottom (the empty box).

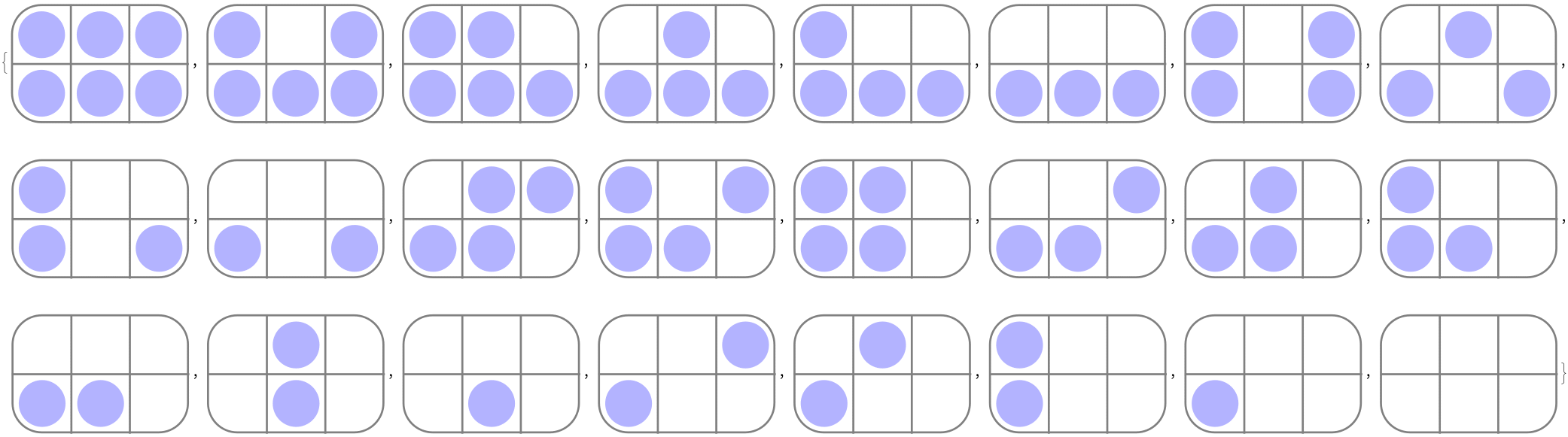
Lets collate these possible options:

That’s a lot more than the “Left-to-Right”, “Right-to-Left”, “Centre-Outwards”, “Outside-In” and “Randomly” the internet considered!

Hopefully when you did the problem with pen and paper you didn’t enumerate all these paths but made some cleaver shortcuts based upon the number you were trying to optimise.

Centers of Mass and All That

So far we have been abstractly dealing with eggs in a box (mathematically we have considered the set \( \{\text{True}, \text{False}\}^6 / (C_2 \times C_2)\). We’ve completely forgotten the point of the problem!

Remember we want to unpack the eggs from the carton in such a way that the carton never gets too imbalanced.

Here we have some interpretation. Should we try to minimise the maximum by which the carton is ever imbalanced (reduce the worst point) or should we allow imbalanced cartons as long as they are short lived and have a smaller average imbalance?

And how do we calculate the imbalance? Its moderately clear that it should have something to do with the the distance of the centre of gravity of the configuration from the middle of the box. However, we might be interested in the the torque that the configuration applies about that point. This subtle difference has to do with whether we consider two configurations with the same centre of gravity but one much heavier than the other (and thus more likely to fall out of our hands) to be the same level of imbalance or not.

All in all, we have four situations on our hands:

1. We minimise the maximum offset of the centre of gravity: \( \min_{\text{paths}}\{\max_{\text{configurations in path}} (|d|)\}\)
2. We minimise the total or average offset of the centre of gravity: \( \min_{\text{paths}}\{\sum_{\text{configurations in path}} (|d|)\}\)
3. We minimise the maximum torque: \( \min_{\text{paths}}\{max_{\text{configurations in path}} (|d|w)\}\)
4. We minimise the total or average torque: \( \min_{\text{paths}}\{\sum_{\text{configurations in path}} (|d|w)\} \)

At this point its a bit tricky to choose. It could even be that all of these options give us the same answer! Lets just call them “metric 1” through to “metric 4” and see what falls out of the maths.

Before we can even talk about torque or centres of gravity we will have to tell the computer the positions of the eggs.

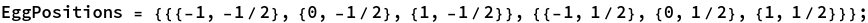
It is now easy to calculate the centre of gravity of any particular configuration.

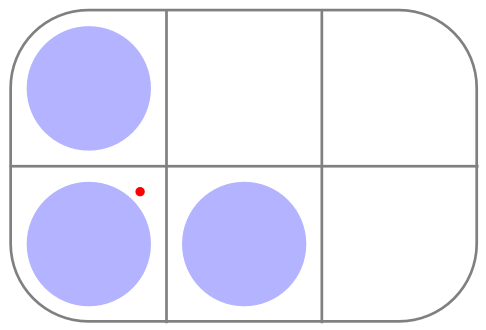
Here’s an example where we graphically draw a configuration and its centre of gravity.

We also have the torque

We can now record the four metrics we can use on a path.

Finding the optimal paths (orders to remove eggs from the carton is now an easy task. We simply optimise on these metrics over all the available paths.

Results

We can take a look at the results that our computations have given us.

Firstly lets consider the metric numbered 1. This metric wanted to minimise the maximum distance the centre of gravity was from the middle of the box. If we look at what this minimum is, we find an interesting thing:

This is just the distance that the middle eggs are from the centre of the box! Clearly the worse time is when there is only one egg left and it is one of the middle ones. Since we can mostly find configurations that do better than this, we’d expect this worst option to appear at the end.

Indeed, if we look at all the possible minimal paths we see that this is the case.

Unforuntately the graphic is a little small and Wolfram Mathematica won’t let me embed a view of them in the graph in this webpage.

However, we can still think a bit about this solution.

Examining the answer it seems that in this case, the internet pundits who got it right were the “Outside-In” guys and some of the “Random” people, some of the time, though almost anything goes as long as you end in the middle.

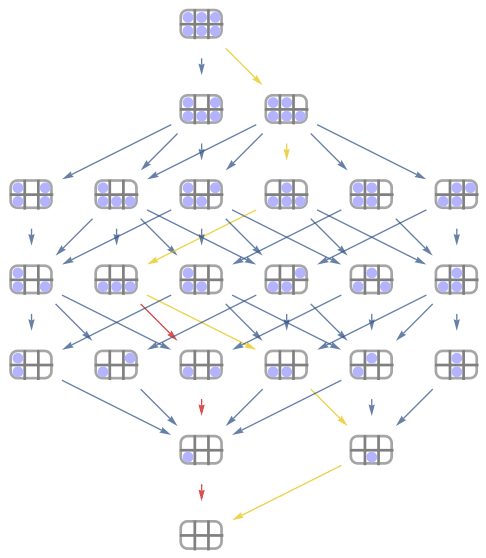
The next easiest metric to examine will be metric 3. Here we want to minimise the maximum torque at any point. Again we look at what minimum was attained.

However, this is not the torque of either configuration with a single egg. This time, there are far fewer possible paths (only two). Lets take a look.

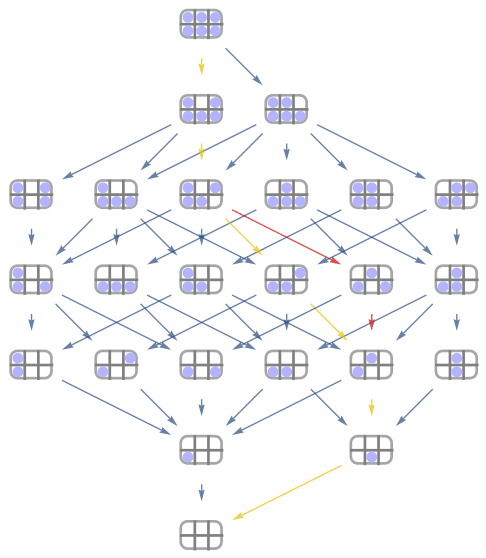
Here we are much more constrained. We want to remove a middle egg first (doesn’t matter which) and leave the other for last. In between there is a particular order to remove eggs, but it doesn’t matter if you remove the third or fourth in that order or swapped.

However, it may be that we should be minimising the sum of the torque or the offset from the centre of gravity. Indeed, if you are removing the eggs one at a time and putting the carton away after using each egg, the likelihood of you dropping your eggs depends on the total amount of imbalance throughout the use of the whole carton. These were the metrics we numbered 2 and 4.

However, as it turns out, the optimum paths for these metrics are exactly the same as for number 3!

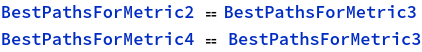
Moreover, both of the optimal paths for metrics 2 through 4 are also optimal for metric 1.

Conclusions

The findings seem clear. No matter which of the metrics we’ve mentioned you choose, you should take one of the two paths below.

Just for fun, here’ s a set of histograms of the various different paths. We see that if you pick your eggs randomly, you are quite likely to take a pretty non - optimal ordering for your eggs.

In the end, though, my colleague and I decided on two entirely different approaches. I usually pick up egg cartons “in the middle of the long side,” so my hand cups one of the centre eggs. This subtly changes the metric and implies that you should remove the far eggs first and then move to the near ones. This does break the symmetry of the situation, but we can still run the same analysis.

On the other hand, my colleague keeps his eggs in the fridge and so always puts them into the fridge and grabs them out from the same small side. He suggested that keeping the centre of gravity as close to his hand to reduce the likelihood of him dropping the eggs forward would be best. This has predictable results as we see below.

Remember that we have removed symmetry from the situation so though this looks like a “right-to-left” win, its also a “left-to-right” suggestion. It probably depends on if you are left or right handed!

In the end it seems that there is no right answer, though many wrong answers. Only one thing is certain: I have spent far more time thinking about this problem than I will ever spend actually packing or unpacking eggs in my lifetime.

You’re welcome.

Footnote

This blog post has been a particularly tricky one to typeset. Eagle-eyed readers will note the difference in the code size and the mysterious blue variables half way through. I’ll probably tinker with it in the months to come, but I really need to move on with my life (thinking about eggs isn’t as much fun as it sounds) so am putting it up here in a “readable” form for now.