Non-induced modular representations of cyclic groups

Liam Jolliffe and Robert A. Spencer

Appeared 14 November 2024 in Communications in Algbra

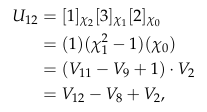
Abstract: We compute the ring of non-induced representations for a cyclic group, \(C_n\), over an arbitrary field and show that it has rank \(\varphi(n)\), where \(\varphi\) is Euler’s totient function - independent of the characteristic of the field. Along the way, we obtain a “pick-a-number” trick; expressing an integer \(n\) as a sum of products of \(p\)-adic digits of related integers.

A draft of this work is available on the ArXiv.

The published version can be found at https://doi.org/10.1080/00927872.2023.2301057.

Cite with BibTex

 @misc{jolliffe2021noninduced,
 author = {Liam Jolliffe and Robert A. Spencer},
 title = {Non-induced modular representations of cyclic groups},
 journal = {Communications in Algebra},
 volume = {0},
 number = {0},
 pages = {1-12},
 year = {2024},
 publisher = {Taylor & Francis},
 doi = {10.1080/00927872.2023.2301057},
 URL = {https://doi.org/10.1080/00927872.2023.2301057},
 eprint = {https://doi.org/10.1080/00927872.2023.2301057}
 }